
Suatu zat yang mempunyai kemampuan mengalir dinamakan fluida. Cairan
adalah salah satu jenis fluida yang mempunyai kerapatan mendekati zat
padat. Letak partikelnya lebih merenggang karena gaya interaksi antar
partikelnya lemah. Gas juga merupakan fluida yang interaksi antar
partikelnya sangat lemah sehingga diabaikan. Dengan demikian
kerapatannya akan lebih kecil.
Karena itu, fluida dapat ditinjau sebagai sistem partikel dan kita dapat
menelaah sifatnya dengan menggunakan konsep mekanika partikel. Apabila
fluida mengalami gaya geser maka akan siap untuk mengalir. Jika kita
mengamati fluida statik, misalnya air di tempayan. Sistem ini tidak
mengalami gaya geser tetapi mempunyai tekanan pada dinding tempayan.
- Berdasarkan uraian di atas, maka pada materi ini akan dibahas dulu
mengenai fluida statik. Pada kegiatan berikutnya akan dibahas secara
khusus fluida dinamik. Pembahasan sering menggunakan konsep umum maupun
prinsip mekanika partikel. Dengan mempelajari materi ini berarti Anda
akan dapat mengkaji sifat fluida statik dan fluida dinamik dengan
menggunakan mekanika partikel. Setelah Anda mempelajari materi ini, Anda
dapat:
Menjelaskan makna hukum utama hidrostatik.
Menggunakan hukum utama hidrostatik untuk menjelaskan sifat-sifat khusus
fluida statik.
Membedakan macam-macam aliran fluida.
Menghitung debit aliran fluida.
Menjelaskan makna hukum Bernoulli.
Menggunakan hukum Bernoulli untuk menjelaskan sifat-sifat aliran fluida.
Menjelaskan masalah fluida pada kehidupan sehari-hari dengan menggunakan
konsep fisika.
FLUIDA STATIKA
Pada kegiatan pertama ini dibahas mengenai fluida statik. Pada
kehidupan sehari-hari, sering digunakan air sebagai contoh. Marilah kita
perhatikan air tenang yang berada di tempayan.

Gambar 1. Gaya-gaya yang bekerja pada dinding tempayan
tempat fluida adalah gaya normal
Cairan yang berada dalam bejana mengalami gaya-gaya yang seimbang
sehingga cairan itu tidak mengalir. Gaya dari sebelah kiri diimbangi
dengan gaya dari sebelah kanan, gaya dari atas ditahan dari bawah.
Cairan yang massanya M menekan dasar bejana dengan gaya sebesar Mg. Gaya
ini tersebar merata pada seluruh permukaan dasar bejana sebagaimana
diperhatikan oleh bagian cairan dalam kolom kecil pada gambar 2. Selama
cairan itu tidak mengalir (dalam keadaan statis), pada cairan tidak ada
gaya geseran sehingga hanya melakukan gaya ke bawah oleh akibat berat
cairan dalam kolom tersebut:
W = m g = ρ V g (1)
di mana ρ adalah kerapatan zat cair dan V adalah volume kolom. Jika V
= h ∆A, kita dapatkan:
W = ρ h ∆A g (2)
Jika berat itu ditopang oleh luasan ∆A, yang sebanding dengan luas
∆A, akibatnya gaya ini tersebar rata di permukaan dasar bejana.
Tekanan sebagai perbandingan gaya dengan luas, seperti diilustrasikan
pada gambar 2.
gaya ρ h ∆A g
p = = = ρ g h (3)
luas ∆A
Di mana p adalah tekanan yang dialami dasar bejana. Dalam satuan
tekanan diukur dalam N/m2, dan dinamai Pascal yang disingkat Pa.

Gambar 2. Cairan setinggi h menekan dasar bejana A
Sebagai contoh, misalnya akan kita cari tekanan dalam Pa, yang
dialami dasar bejana cairan dengan ρ = 670 kg/m3 dan dalamnya 46 cm.
p = ρ g h = (670 kg/m3) (9,8 m/s2) (0,46 m)
= 3020 kg.m/s2 = 3020 n/m2 = 3020 pa
Tekanan adalah kuantitas skalar tanpa arah. Gaya yang menghasilkan
tekanan yang bekerja pada permukaan adalah vektor yang arahnya selalu
tegak lurus ke permukaan. Kita dapat menggunakan keadaan setimbang
gaya-gaya yang bekerja pada bagian kecil cairan, seperti dilukiskan pada
gambar 3.

Gambar 3. Keseimbangan gaya pada bagian kecil cairan.
Bagian kecil cairan yang tebalnya ∆A dan luas permukaan bagian atas
(ada bagian bawah) A serta luas sisi lainnya A mengalami keseimbangan
gaya. Dalam hal ini cairan tidak mengalami pergolakan yang mengakibatkan
cairan mengalir. Tiap bagian dari cairan mestilah diam. Tekanan yang
dilakukan bagian cairan lain pada bagian kecil cairan tersebut yang
dilakukan oleh gaya-gaya F3 dan F4 saling meniadakan, demikian pula oleh
gaya-gaya F5 dan F6. Gaya F2 mestilah cukup besar terhadap F1 agar
dapat menopang bagian cairan tersebut.
Karena F3 = F4 dan F5 = F6, maka p3 (=F3/A2) = p4 (=F4/A2) dan p5
(=F5/A2) = p6 (F6/A2)
Sekarang, karena F2 > F1, maka
p2 A1 . p1 A1 = ρ g A1 ∆h
p2 . p1 = ρ g ∆h
atau
∆p = ρ g ∆h (4)
Jadi, apabila kerapatannya konstan, perubahan tekanan di antara dua
titik di dalam cairan berbanding lurus dengan perbedaan kedalamannya.
Pada kedalaman yang sama mempunyai tekanan yang sama. Selama variasi
tekanan di dalam cairan statis hanya tergantung pada kedalamannya, maka
penambahan tekanan dari luar yang dilakukan pada permukaan cairan,
misalnya karena perubahan tekanan atmosfer atau tekanan piston, mestilah
merupakan penambahan tekanan pada semua titik dalam cairan, seperti
dikemukakan oleh Blaise Pascal (1623-1662), yang dikenal sebagai Hukum
Pascal.
Tekanan yang dilakukan pada cairan dalam ruang tertutup, akan
diteruskan kemana-mana sama besarnya termasuk dinding tempatnya.
Apabila kerapatan ρ (massa jenis) sangat kecil, misalnya fluida
berbentuk gas, maka perbedaan tekanan pada dua titik di dalam fluida
dapat diabaikan. Jadi di dalam suatu bejana yang berisi gas, tekanan gas
di mana-mana adalah sama. Hal ini tentu saja bukan untuk ∆h yang sangat
besar. Tekanan dari udara sangat bervariasi untuk ketinggian yang besar
dalam atmosfer. Dalam kenyataan, kerapatan ρ berbeda pada ketinggian
yang tidak sama dan ρ ini hendaklah kita ketahui sebagai fungsi dari h
sebelum persamaan 3 di atas kita pergunakan.
Marilah kita perhatikan hal berikut ini. Andaikan ke dalam pipa
berbentuk U dimasukkan dua jenis cairan yang tidak dapat bercampur
secara sempurna, misalnya air dengan minyak tanah.

Gambar 4. Pipa berbentuk U berisi dua jenis cairan.
Setelah cairan yang kerapatannya ρ1 dimasukkan ke dalam pipa, cairan
yang kedua dengan kerapatan ρ2 (di mana ρ1 > ρ2) dimasukkan ke salah
satu pipa sehingga permukaan cairan yang pertama turun setinggi 1 di
bawah cairan yang kedua itu, sedangkan permukaan lainnya naik setinggi 1
seperti dilukiskan pada gambar 4 di atas. Akan kita tentukan
perbandingan kerapatan kedua jenis cairan tersebut. Pada gambar 4 titik C
menyatakan keseimbangan tekanan. Tekanan di C yang dilakukan cairan di
atasnya adalah
Untuk cairan pertama : p1 g 2 1
Untuk cairan kedua : p1 g 2 1
Sehingga :
ρ1 g 2 1 = ρ2 g (d + 2 1)
atau
ρ2 2 1
=
ρ1 d + 2 1
Perbandingan kerapatan suatu bahan terhadap kerapatan air dinamakan
kerapatan relatif atau gravitas spesifik dari bahan tersebut.
Archimedes mendapatkan suatu prinsip sebagai berikut. Apabila suatu
benda dicelupkan ke dalam cairan (seluruhnya atau sebagian), benda itu
mengalami gaya ke atas sebesar berat cairan yang dipindahkannya.
Apabila sebuah benda dicelupkan ke dalam cairan, seperti ditunjukkan
dalam gambar 5, total gaya ke atas atau gaya angkat, dilakukan pada
benda. Akibat gaya ini terdapat perbedaan tekanan pada bagian bawah dan
bagian atas benda. Selama tekanan ini tergantung pada kedalaman cairan,
dengan mudah dapat kita hitung gaya ke atas untuk sederhana, antara lain
untuk balok tegar di mana salah satu permukaannya horizontal.

Gambar 5. Gaya-gaya yang dialami benda di dalam cairan.
Benda yang bentuknya sembarang, agak sulit kita menentukan tekanan
karena bervariasinya titik-titik permukaan benda. Untuk itu prinsip
Archimedes sangat membantu. Andaikan benda dikeluarkan dari dalam cairan
akan menggantikan tempat benda sebanyak tempat yang tadinya ditempati
oleh benda. Jika volume tempat benda itu telah diisi oleh cairan, ini
menunjukkan bahwa adanya keseimbangan gaya yang terjadi antar cairan
penyelubung dengan bagian cairan yang menggantikan tempat benda
tersebut. Jadi gaya netto yang arahnya ke atas adalah sama dengan m1 g,
di mana m1 adalah massa cairan yang mengisi volume yang ditinggalkan
oleh benda.
Sekarang kita tinggalkan pengandaian tadi dengan benda sesungguhnya
yang massanya mo. Cairan mestilah melakukan kontak dengan setiap titik
pada permukaan benda yang memberikan gaya-gaya sama di mana-mana. Gaya
ini mestilah sama dengan gaya penopang cairan yang volumenya adalah
sama. Gaya ini adalah gaya angkat (ke atas) yang besar.
Fb = mf g = ρ1 Vg
(5)
Di mana m1 adalah massa cairan yang dipindahkan oleh benda yang
tercelup ke dalam cairan adalah kerapatan cairan. Gaya angkat ini
arahnya vertikal ke atas.
Persamaan 5 dinamakan Prinsip Archimedes yang dikemukakan oleh
Archimedes pada tahun 250 SM. Jika gaya ke atas lebih kecil daripada
berat benda yang dicelupkan, mala benda itu akan tenggelam. Jika berat
benda lebih kecil daripada gaya ke atas, benda itu akan terapung.
Seandainya ρo adalah kerapatan benda, dengan volume V, maka beratnya
W = mo g = ρo V g
Gaya ke atas dinyatakan oleh persamaan 5.
Fb = ρ1 V g (6)
Netto gaya ke atas ketika benda semuanya tercelup dalam cairan
Fnet = Fb . W =( ρf. ρo) V g (7)
Jadi benda dengan kerapatan lebih besar dari kerapatan cairan akan
tenggelam, dan yang lebih kecil akan terapung.










 20.15
20.15
 Roffian
Roffian









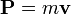
 bergerak dengan kecepatan masing-masing adalah
bergerak dengan kecepatan masing-masing adalah  ,
maka kecepatan pusat massa sistem tersebut adalah :
,
maka kecepatan pusat massa sistem tersebut adalah :
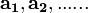 ,
maka percepatan pusat massa sistem tersebut adalah :
,
maka percepatan pusat massa sistem tersebut adalah :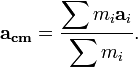
 ,
maka benda-benda tersebut masing-masing memiliki percepatan :
,
maka benda-benda tersebut masing-masing memiliki percepatan :

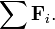 merupakan notasi yang menyatakan resultan gaya yang bekerja pada sistem
tersebut. Jika resultan gaya yang bekerja pada sistem bernilai nol (
merupakan notasi yang menyatakan resultan gaya yang bekerja pada sistem
tersebut. Jika resultan gaya yang bekerja pada sistem bernilai nol ( ),
maka sistem tersebut tidak dipercepat (
),
maka sistem tersebut tidak dipercepat ( ).
Jika sistem tidak dipercepat, artinya sistem tersebut kecepatan pusat
massa sistem tersebut konstan (
).
Jika sistem tidak dipercepat, artinya sistem tersebut kecepatan pusat
massa sistem tersebut konstan ( ).
Jadi dapat disimpulkan bahwa :
).
Jadi dapat disimpulkan bahwa :


































